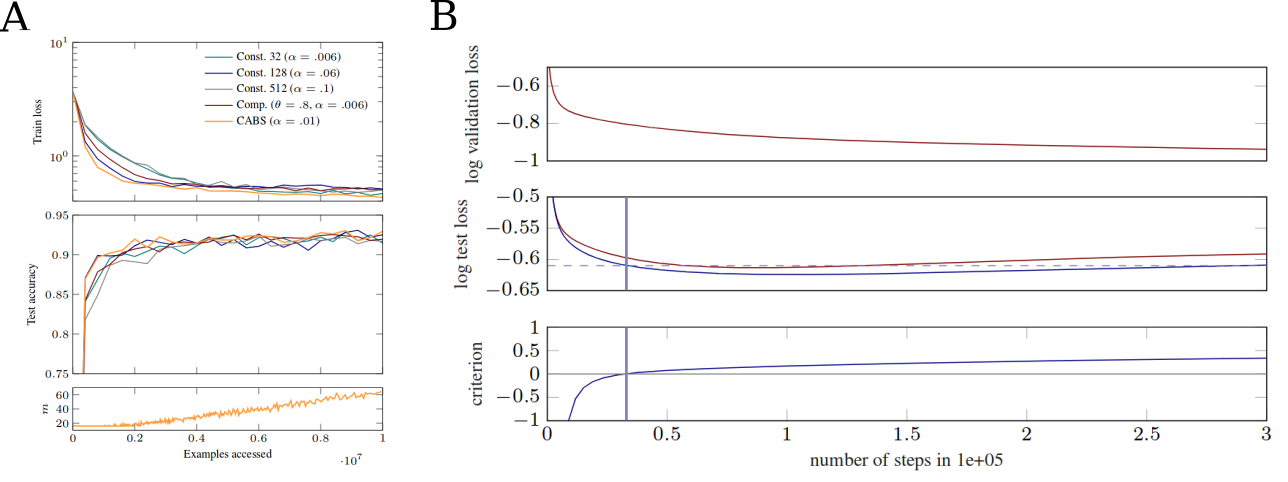
(A) Effects of adaptive batch size. Training loss, test accuracy and batch size from top to bottom against accessed examples for the Street View House Numbers dataset. Green, blue and grey are constant batch sizes, red uses an alternative batch size adaptation criterion, orange, corresponds to the coupled adaptive batch size (CAPS) introduced in [ ]. (B) Top and middle are validation and test loss for validation based stopping (red) and evidence based criterion [ ]. Criterion is shown in bottom. The blue bar is the proposed stopping point.
Machine Learning is an important tool for Computer Vision. After the success of Deep Neural Networks(DNN)s in image classification tasks, many other tasks were solved using DNNs. However, working with deep learning, researchers are confronted with many problems related to implementation, hyper-parameter selection, training time, training data and computation time that seek to be solved.
Writing code for a deep learning project is often very time consuming.. Even though, Caffe has many disadvantages in comparison to other frameworks, many works are still written using Caffe. For example it's missing a full Python interface and relies heavily on configuration files. To address these issues we developed Barrista [ ], a wrapper for Caffe, that offers full pythonic control over Caffe.
Another difficulty that researchers working on deep learning have to face is the large amount of training data needed. This problem becomes even more serious, because a validation and test set is needed to avoid over-fitting. In new work, we show an alternative to a validation set for early stopping. The criterion depends on fast-to-compute local statistics of the gradients. By these means it is possible to decrease the problem of small training sets [ ].
Training neural networks comes with many hyper-parameters that must be chosen, which is often a time consuming process. Mini-batch stochastic gradient descent and variants thereof are the standard for training neural networks. The batch size is commonly chosen based on empirical inspection and practical reasons. However, the batech size determines the variance of gradient estimates and therefore influences strongly the behavior of the optimization process. Further, the variance changes during optimization. Because of these reasons we propose a dynamic batch size adaptation in [ ]. It leads to faster convergence and simplifies the learning rate tuning.
Many Computer Vision problems can be formulated as a graph partitioning and node labeling task. But the resulting problem, known as minimum cost node labeling multicut problem, is proven to be NP-hard. In order to get a reasonably fast Computer Vision algorithm heuristics are needed to solve minimum cost node labeling multicut problems. In [ ] we propose two local search algorithms that converge to a local optimum. Both of which achieve state-of-the-art accuracy achieved for the tasks mentioned above. The general formulation enables the usage of this method by researchers for many different tasks.
