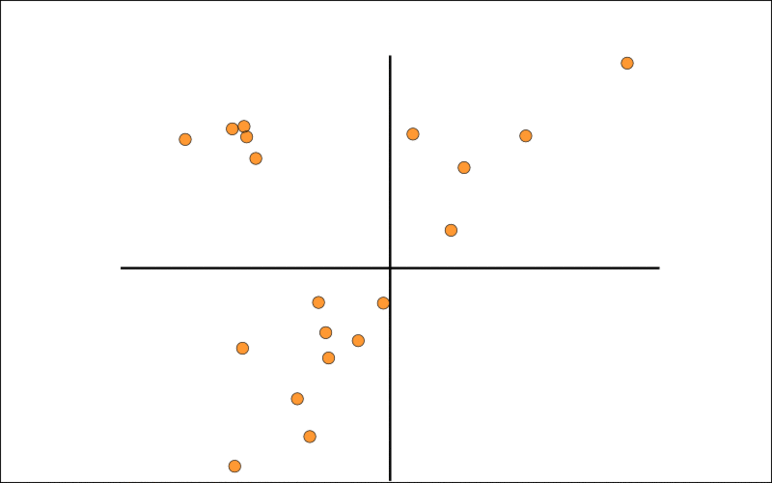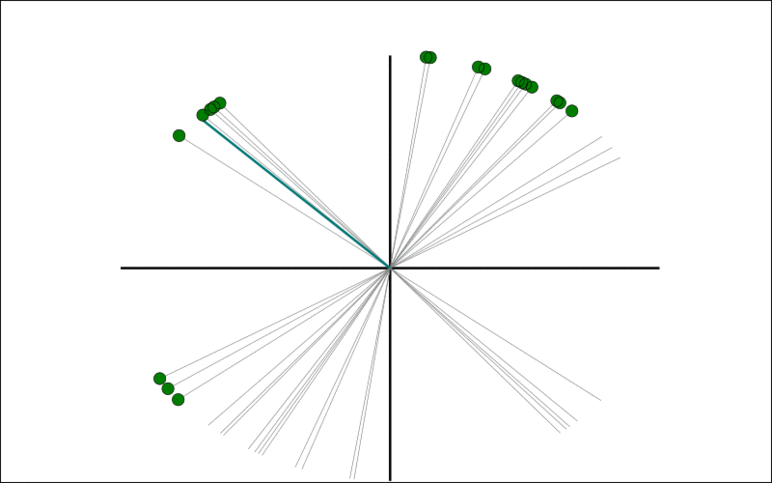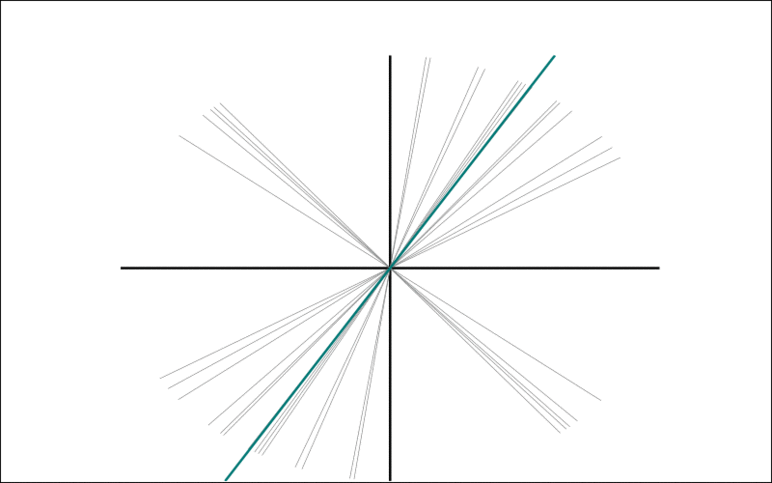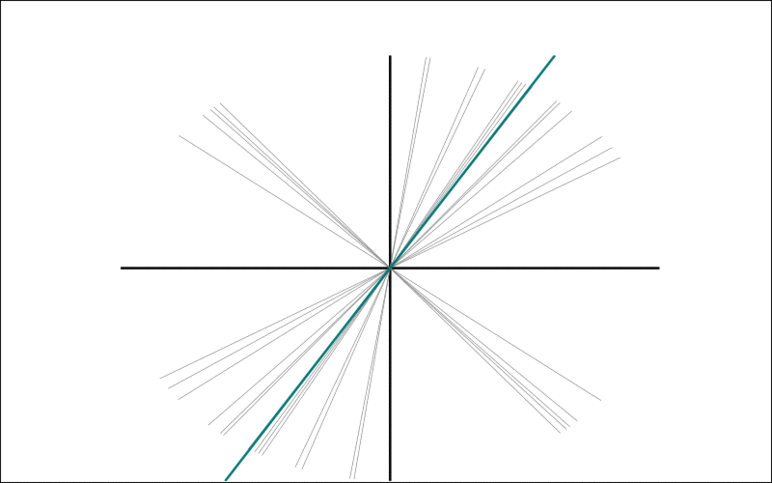
The animation show the Trimmed Grassmann Average (TGA) algorithm on synthetic data (orange circles). The algorithm is initialized roughly orthogonal to the correct component. In each iteration, all observations are given a sign to be as similar as possible to the current component estimate. The component (blue line) is then updated as the trimmed mean of the re-signed data (green circles). This is repeated until convergence.
There are several ways to approach robust principal component analysis (RPCA). In early work [ ] we noted that PCA constructs a linear subspace that minimizes least squares reconstruction error of the data. Since least squares is not robust to ourliers, neither is standard PCA. We reformulated the reconstruction term robustly and solved for the subspace that minimized a robust error term. The approach worked well but was computationally expensive.
As the collection of large datasets becomes increasingly automated, the occurrence of outliers will increase -- big data implies big outliers. As a scalable approach to robust PCA we propose to compute the average subspace spanned by the data; this can then be made robust by computing robust averages [ ].
We note that in a zero-mean dataset, each observation spans a one-dimensional subspace, giving a point on the Grassmann manifold. We show that the average subspace corresponds to the leading principal component for Gaussian data. We provide a simple algorithm for computing this Grassmann Average (GA), and show that the subspace estimate is less sensitive to outliers than PCA for general distributions. Because averages can be efficiently computed, we immediately gain scalability. We exploit robust averaging to formulate the Robust Grassmann Average (RGA) as a form of robust PCA. The resulting Trimmed Grassmann Average (TGA) is appropriate for computer vision because it is robust to pixel outliers. The algorithm has linear computational complexity and minimal memory requirements. We demonstrate TGA for background modeling, video restoration, and shadow removal. We show scalability by performing robust PCA on the entire Star Wars IV movie; a task beyond any current method.
This page provides source code and video material for the paper Grassmann Averages for Scalable Robust PCA.
We provide implementations for the Grassmann Average, the Trimmed Grassmann Average, and the Grassmann Median. We the simplest is the Matlab implementation used in the CVPR 2014 paper, but we also provide a faster C++ implementation, which can be used either directly from C++ or through a Matlab wrapper interface. The code is available for download below. Any feedback is much appreciated and can be send to Søren Hauberg.
C++ Implementation
A highly parallel C++ implementation of the Grassmann averages are available at the Tübingen MPI-IS Github. This includes both a C++ library and a Matlab interface. This is the recommended implementation of the algorithms.
Matlab Implementation
The simplest implementation is done in pure Matlab, with a C++ implementation of trimmed averages. This implementation was used for the CVPR 2014 paper. With the release of the pure C++ implementation, this code is mostly useful for understanding the basic algorithms.
Example Code
As a simple example, we will first generate samples from a random Gaussian distribution, and then estimate its leading component.
D = 2; % we consider a two-dimensional problem N = 100; % we will generate 100 observations %% Generate a random Covariance matrix tmp = randn(D); Sigma = tmp.' * tmp; %% Sample from the corresponding Gaussian X = mvnrnd(zeros(D, 1), Sigma, N); %% Estimate the leading component comp = grassmann_average(X, 1); % the second input is the number of component to estimate %% Plot the results plot(X(:, 1), X(:, 2), 'ko', 'markerfacecolor', [255,153,51]./255); axis equal hold on plot(3*[-comp(1), comp(1)], 3*[-comp(2), comp(2)], 'k', 'linewidth', 2) hold off axis off
This produces a plot like the figure below:

Download
The initial version of the Matlab code is now available: grassmann_averages-0.3.zip. For questions or comments please contact Søren Hauberg.
