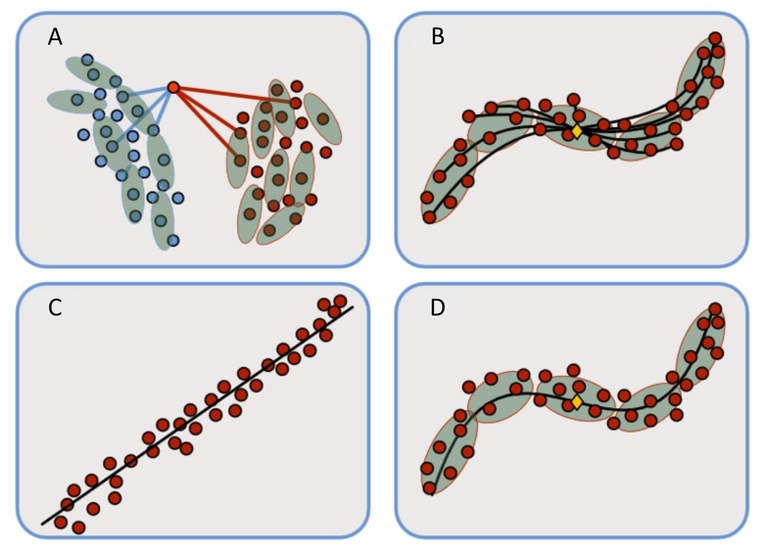
A: In multi-metric learning, different distance measures (shown by the ellipsoids) are aplied in different regions of the feature space. While succesful in classification, the idea is non-metric, which has prevented the idea from being generalized to other tasks. B: Shortest paths according to the smoothly changing distance measure we propose. Here they are computed between the mean and each data point. C: Data is mapped to the Euclidean tangent space and the first principal component is computed. D: The principal component is mapped back to the feature space.
Statistics relies on measuring distances. This simple observation has lead to the idea that the distance measure should change locally to better adapt to the problem. With this strategy even simple classifiers can be competitive with the state-of-the-art because the distance measure locally adapts to the structure of the data. This idea, which is known as Multi-metric Learning, is illustrated in A.
One mathematical issue with this model is that the applied distance measure is not metric as it is not symmetric and the triangle inequality is violated. This has prevented the idea from being used for non-classification tasks, such as regression and dimensionality reduction, where metricity is essential.
In previous models, a local distance function (in the form of a metric tensor) is learned at a discrete set of points. We define a smooth version of this model by defining the metric tensor at any point as a smoothly changing weighted average of the learned metric tensors. From the smoothness we show that the resulting feature space becomes a Riemannian manifold. Since such spaces are metric spaces, we have avoided the above-mentioned issue with previous models.
On Riemannian manifolds, statistical operations such as regression, PCA, Kalman filters, etc., are well-defined and algorithms are readily available. We can, thus, extend multi-metric learning to be useful for these tasks. Note that to achieve this, we only have to ensure that the distance measure changes smoothly throughout the feature space, which is a very natural assumption.
The basic idea behind most statistical operations on manifolds is to express the data in a local tangent space of the manifold and perform Euclidean statistics in this space. As is common, we first compute the mean of the data (defined as the minimizer of the sum of squared distances to the data) and express the data in the tangent at this point. Here a Euclidean model, e.g. PCA, is learned and the resulting model is mapped back to the manifold (which in this case is the original feature space). This process is shown in B-D.
To perform these operations we need algorithms for computing shortest paths and distances according to the smoothly changing distance measure. Furthermore we need algorithms for mapping back and forth between local tangent spaces. We show how these problems can be formulated as the solution to a system of ordinary differential equations.
An example implementation is available here. See the README.txt file for details.
